Notes
two concentric circles solution
Solution to the Two Concentric Circles Puzzle
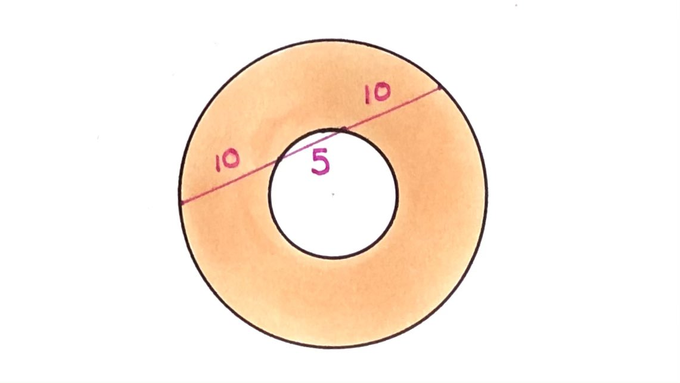
These two circles have the same centre. What’s the shaded area?
Solution by Pythagoras Theorem
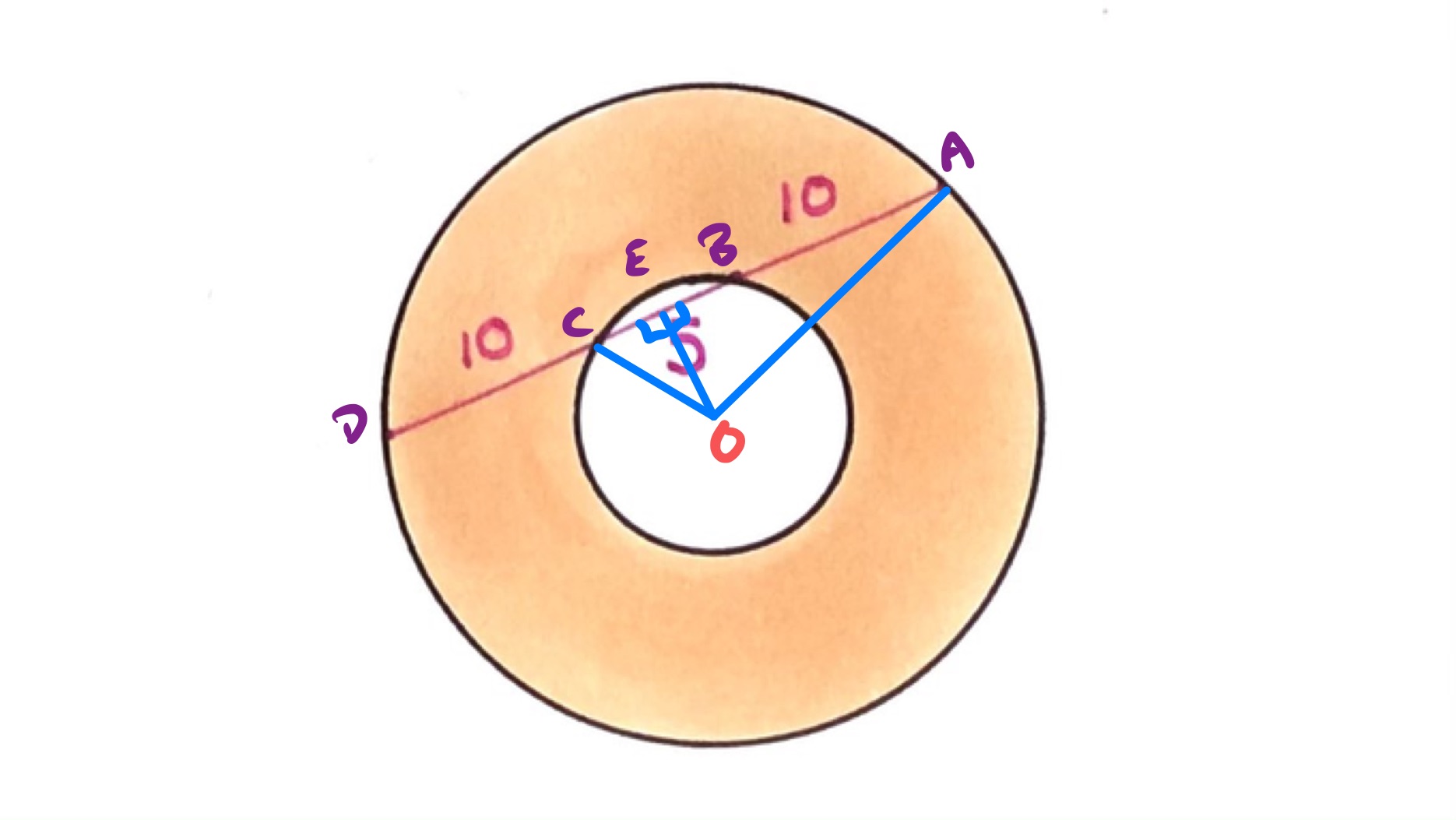
Let us write for the radius of the outer circle, so on the diagram above we have , and for the radius of the inner circle, so . In the diagram, is the midpoint of the chord and let us write for the distance . Note that meets the line at a right-angle.
Since is a right-angled triangle, Pythagoras' Theorem says that
Since is a right-angled triangle, Pythagoras’ Theorem also says that
Eliminating from these gives
We can directly calculate that, or we can use the difference of two squares to write it as .
The area we want to calculate is the area of the large circle minus the area of the smaller one. This is:
Solution by Intersecting Chords Theorem
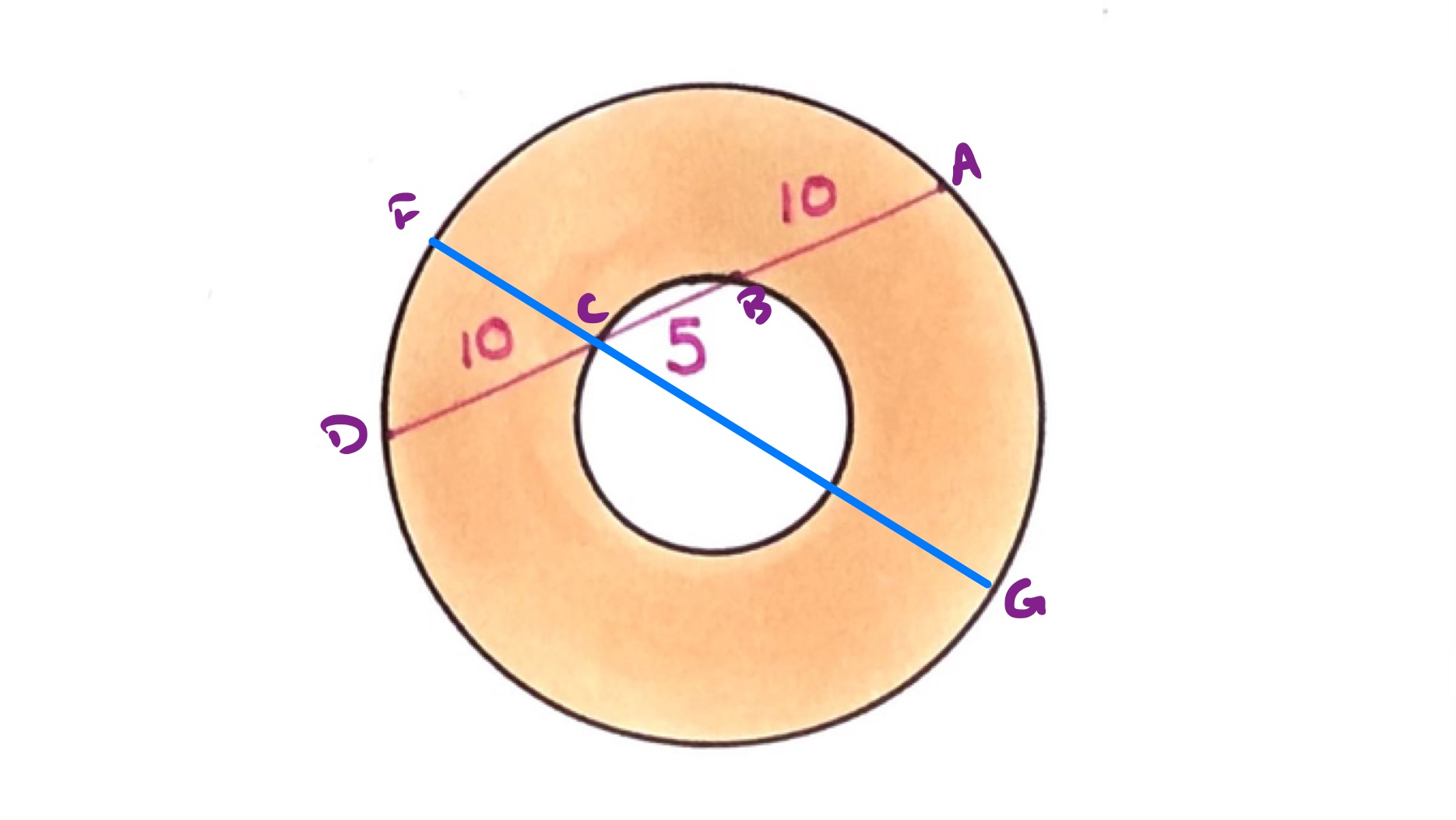
In this diagram, the line is chosen to be the diameter that passes through .
The intersecting chords theorem says that in the above diagram then:
With and as above, then and so then
Hence and so the orange area can be calculated as: